前缀和算法

一维数组前缀和

原理

给定一个 a 数组，请求出它的前缀和数组 s ：

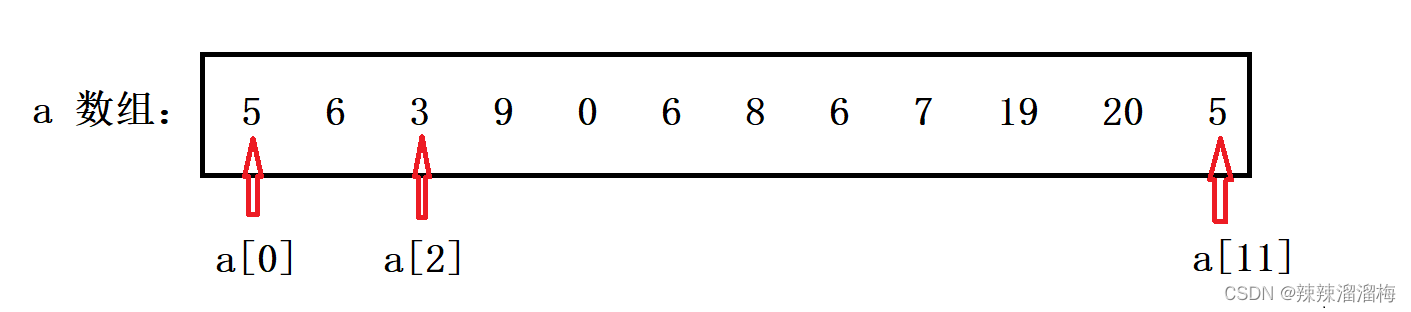
那么 a 数组的前缀和数组为：

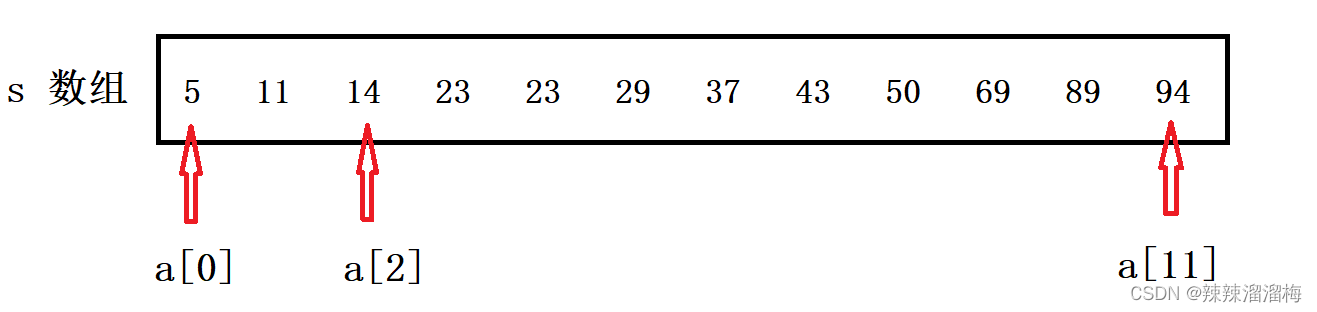
a 数组与 s 数组之间满足：s[ i ] = a[ 0 ] + a[ 1 ] + a[ 2 ] + … + a[ i ]
但是，由于我们在计算前缀和时，为了更加方便，我们会将数组下标从 1 开始存入和读取。
所以，我们的 s 前缀和数组为： s[ i ] = a[ 1 ] + a[ 2 ] + … + a[ i ]

应用
若是要求某个区间的和该怎么办？
用以上的例子，我们想求 a 数组中下标从 3 到 6 的数值的和。如下图：

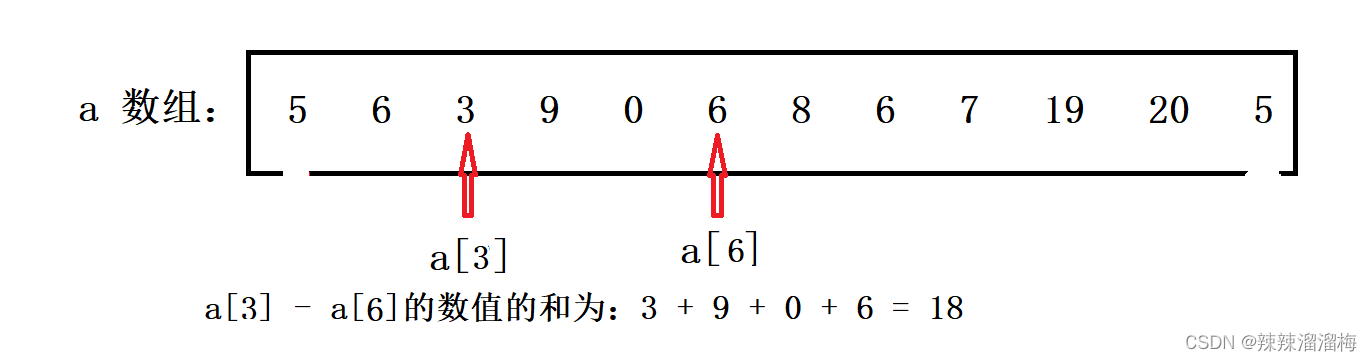
用前缀和原理分析可知：a[ 3 ] + a[ 4 ] + a[ 5 ] + a[ 6 ] = s[ 6 ] - s[ 2 ]
根据以上原理，很容易实现代码。

示例题目

题目：前缀和
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问，每个询问输入一对 l,r。
对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数，表示整数数列。
接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。
输出格式
共 m 行，每行输出一个询问的结果。
数据范围
1≤l≤r≤n ,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10
————————————————

#include<iostream>

using namespace std;

const int N = 100010;

int n, m;
int a[N], s[N];

int main()
{
	scanf("%d%d", &n, &m);

	for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);	
	for(int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];

	while(m --)
	{
		int l, r;
		scanf("%d%d", &l, &r);
		printf("%d\n", s[r] - s[l - 1]);
	}

	return 0;
}